Azul AI

Table of Contents

An “AI” that can play the board game Azul better than a Human.

Azul is a 2-4 player board game in which the aim is to collect coloured tiles and arrange them on a wall to score points. The game typically takes 5 or 6 rounds, after which a winner is decided. Here is a detailed description of the rules.

This post outlines an AI that can play Azul as good as, if not better than a human. Its not really AI though, it hasn’t learned how to play (yet) and it just follows an algorithm to determine the best move. I think it is quite interesting though.

Don’t want to read, play it here.

Game development #

The game is implemented in Typescript as it allows easy GUI development. A single class is used to represent the game, containing the tilebag, factories, player boards, a list of available moves and other properties required to run the game.

export class GameState {
tilebag: Array<Tile> = [];
factory: Array<Array<Tile>> = [];
playerBoards: Array<PlayerBoard> = [];
availableMoves: Array<Move> = [];
...
}

The PlayerBoard class looks something like:

export class PlayerBoard {
wall: Array<Array<Tile>> = [[],[],[],[],[]];
lines: Array<Array<Tile>> = [[],[],[],[],[]];
floor: Array<Tile> = [];
score : number = 0;
...

The GameState class contains a number of functions to manipulate it and complete a game:

export class GameState {
...
newGame (nPlayers: number):void {...}
newRound ():void {...}
nextTurn() :boolean {...}
endRound() : boolean {...}
getMoves(): void {...}
playMove(move: Move): void {...}
createFactories(): void {...}
moveToWall(player:number, wall:Array<Array<Tile>>): number {...}
smart_clone(move:Move): GameState {...}
}

One important function for the AI is the ability to clone the game state, which will be explained later on.

The game state is decoupled from the game logic, so it is possible to use it for the GUI, AI players and CLI games.

The repo for the game implementation is https://github.com/domw95/azul-tiles.

GUI #

The GUI displays the current game state and runs through the game logic according to user input. A state machine tracks the current game state and transitions to other states with mouse-clicks on the screen. The start of a game looks like this:

Not quite as pretty as the original…

The game is played by clicking on a desired tile from a factory, then clicking on the line (or floor) where the tile(s) is to be placed.

The source for the game GUI is https://github.com/domw95/tiles-web.

AI development #

The AI is based on the minimax algorithm. The general idea is to look ahead a number of turns (by the both the AI and its opponent), and pick the move that guarantees a minimum outcome, regardless of the moves the opponent makes. To look ahead a number of turns, a game tree needs constructing.

Game tree #

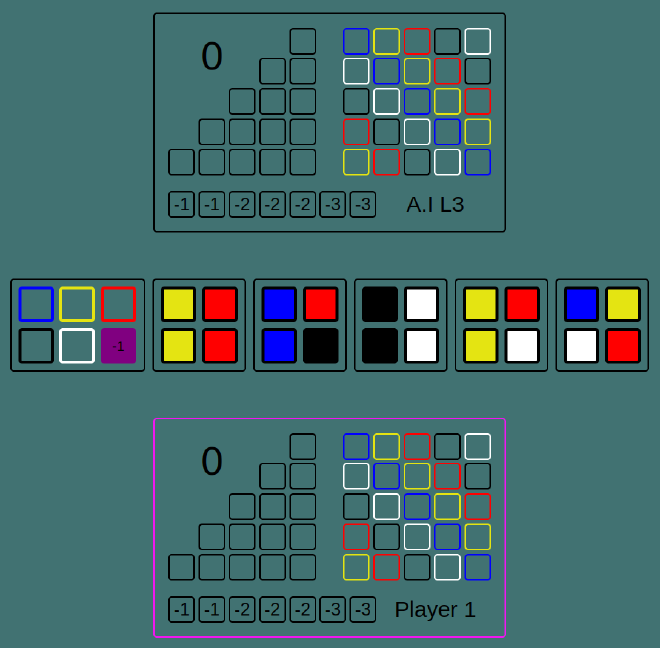
The possible outcomes from a certain position in Azul (and many other games) can be represented by a game tree. Each node of the tree represents a game state, each branch is a possible move to transfer to a new game state and each state has an associated value.

The value represents how good the game state is for the each player. For example, 0 is equal, positive is good for the AI, negative is good for its opponent.

Below is an example of a game tree with 2 possible moves each turn.

graph TB; A((0))-->B((2)) A-->C(("-1")); B-->D(("-5")) B-->E((4)) C-->F((3)) C-->G((2))

The AI is about to play a move, and is trying to maximise the outcome. The game is currently equal, as represented by the 0 in the root node.

If the AI were to only consider 1 move in advance, it would see that the game state after the left move (2) is worth more than the right move (-1), so it would appear to be better.

However, the opponent can respond with a move aiming to minimise the score. For each of the possible first moves, the minimum score would then either be -5 or 2. Now the righthand move looks more promising for the AI for its turn. This lookahead process could continue for the 3rd, 4th turn etc until the end of the game.

The minimax algorithm essentially follows this thought process but with a more rigorous approach.

Minimax #

First a game tree is constructed to a certain depth and then the state of each node at that depth is assessed and assigned a value:

graph TB; A((_))-->B(("_")) A-->C(("_")); B-->D(("_")) B-->E((_)) C-->F((_)) C-->G((\_)) D-->I(("-3")) D-->J(("-2")) E-->K((4)) E-->L((5)) F-->M((1)) F-->N((3)) G-->O((2)) G-->P((2)) Q["1 (MAX)"]-->R["2 (MIN)"]-->S["3 (MAX)"]

Then, for each node with child nodes, either the minimum or maximum (depending on the player acting from the node) of the child nodes is chosen as the node value.

This happens recursively from the root, but effectively bottom to top, until the root node has a value and an optimal move.

Below is the same tree diagram with the minimax values assigned. The red nodes are the ones chosen as the best move at each turn.

graph TB; A((2))-->B(("-2")) A-->C(("2")) B-->D(("-2")):::highlight B-->E((5)) C:::highlight-->F((3)) C-->G(("2")) D-->I(("-3")) D-->J(("-2")):::highlight E-->K((4)) E-->L((5)):::highlight F-->M((1)) F-->N((3)):::highlight G:::highlight-->O((2)):::highlight G-->P((2)) Q["1 (MAX)"]-->R["2 (MIN)"]-->S["3 (MAX)"] classDef highlight fill:#f9f,stroke:#333,stroke-width:1px;

Based on this depth=3 search, the best move for the AI is the righthand move, with a guaranteed minimum outcome of 2, assuming optimal play.

Game tree construction #

A game tree can be constructed from the root node (current game state) recursively up to a certain depth. The algorithm is roughly as follows:

For each node, starting from the root:

Generate list of possible moves from current game state
Create a child node / game state for each of the possible moves (by cloning the current state and playing the move)
If at required depth: stop, otherwise repeat for each child node

Azul #

To implement minimax AI for Azul therefore requires:

A way of listing possible moves at each turn
A method to clone the game state
A function to assign a value to each game state.

The first is implicitly part of the game implementation already, the second is easy to add but the third is more tricky.

Value function #

The value function takes the game state as an input and returns a score from the AI’s perspective representing how good the current situation is. The simplest way to do this is to consider how many points each player would score if the round were to end immediately, and return the difference between them.

As required, a value of 0 would be equal, positive is good for the AI and negative is good for its opponent.

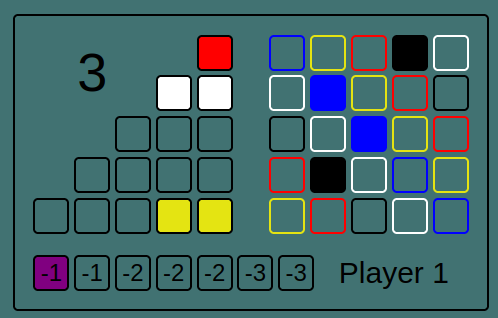
For each player, the function clones the current wall, copies tiles from each full line, and counts up the score from each tile placed in the wall. This score is added to the players actual score from previous rounds.

Using the board below as an example. If the tiles from full lines were moved over to the wall the player would receive 2 points for red, 2 for white, 0 for yellow (not full) and -1 for the floor. Combined with the current score of 3, the board value is 6.

If the opponents value is 8, the game state value would therefore be -2.

Azul player board — Player board during round 2. The value assigned is 6

The fact that a value can be assigned relatively easily in Azul makes this type of AI much simpler to implement. Games without explicit scores / values can be much harder to create value functions for (e.g chess).

However, it also doesn’t consider possible future scores from row, column or colour combinations (unless they are immediately attainable), so there is room for improvement.

AI Implementation #

The minimax algorithm outlined in the previous section is able to take the Azul game state, look a defined number of moves ahead, and pick an optimal move with a guaranteed minimum outcome. This warrants the question: how many moves to lookahead?

The simple answer is: as far as possible. The limits for tree depth are time, computer memory and the end of the round occurring. The end of round isn’t a limit as such, but is a useful indicator to tell the algorithm to stop. I shall assume there is enough RAM, so the only real limit is time.

The problem is that at a fixed depth, the algorithm runs for different durations depending on the game state. At the start of a round there can be 100 moves to choose from, maybe 90 and 80 on turns 2 and 3. This is 100x90x80 = 720,000 leaf nodes to evaluate. Towards the end of the round, there will be less than 10 moves each turn, so less than 1000 leaf nodes. Selecting a fixed depth to limit the time taken will cap the possible performance towards the end of the round.

Another issue is that AI’s opponent may have to wait a long time for it to calculate moves.

Deepening #

The solution is to sequentially search deeper and deeper trees until a time limit expires. Starting with a depth of 1, the best move would be found and saved, then depth = 2 etc. If the time expires during a tree traversal, the best move from the previous depth would be used.

The table below shows the results of a round between 2 minimax AI players using deepening with 1 second to play against each other. Full depth means that all leaf nodes at the search depth result in the end of the round, so the minimum score is guaranteed at the end of the round.

Turn	Depth	Moves	Leaf Nodes	Full Depth
1	2	78	5616	no
2	2	72	3810	no
3	2	55	2500	no
4	3	45	33436	no
5	3	32	15124	no
6	4	28	50985	no
7	5	18	50938	no
8	5	16	6931	yes
9	4	9	305	yes
10	3	7	46	yes
11	2	4	8	yes
12	1	2	2	yes

For performance reasons, it is also recommended to reuse and expand the tree from the previous depth, which also enables other enhancements.

AI Improvements #

Aside from code improvements (of which I am sure there are many), there are a few ways of speeding up the minimax algorithm to allow deeper trees to be traversed in the given time. The most common is alpha-beta pruning.

Alpha-Beta pruning #

Alpha-beta pruning achieves the same result as minimax but reduces the number of nodes that need to be evaluated. The idea is to track the current worst guaranteed outcome for each player (alpha and beta) and to use them to eliminate branches from the search.

The wikipedia article likely explains it much better than I could.

The game tree is no longer created at the start, instead it is recursively generated as required, with no unnecessary calculations for nodes that are pruned.

Move sorting #

One way of improving the performance of alpha-beta pruning is to sort the moves from best to worse before traversing the tree. This way it is more likely that more branches are pruned, reducing the time to search the tree.

It is not necessarily easy to determine the relative value of each move and sort them efficiently, but there is a trick when using the deepening method above. The idea is to utilise the results from the previous depths search to sort the child nodes.

The depth 1 tree is searched as normal, then all the child nodes are sorted according to their value (best to worst, left to right). Then the depth 2 tree is searched (by expanding the depth 1 tree), with the most promising children traversed first, increasing the chance of pruning. The process continues with depth 3, 4 etc.

To see how all of this is implemented, look at the source https://github.com/domw95/minimaxer.

Comparison #

The table below shows how many leaf nodes are evaluated at each depth at the start of a game when using the deepening approach for minimax, alpha-beta pruning and with presorting moves. Each method achieves the same result, but analysing fewer nodes is generally quicker.

Method	1	2	3	4
Minimax	84	6552	396552	N/A
Alpha-beta pruning	84	393	9401	41275
Alpha-beta + presort	84	316	7373	36754

Clearly alpha-beta pruning is able to greatly reduce the number of nodes that need analysing. At a depth of 2 it is a factor of ~16 less, at a depth of 3 it is ~400x.

Minimax at a depth of 4 has to analyse so many nodes that it takes minutes and runs out of memory (32GB) before completing.

Presorting alpha-beta provides a small boost, but comes at the expense of more calculations, so whether it is beneficial during time constraints needs to be checked.

Head to head #

The best way of comparing 2 AI algorithms is to have them play each other for a number of games and see which one claims the most victories. To make it fair, for each random game that is generated, each AI gets a chance to play first.

Each AI is given up to 100 ms to pick a move.

Minimax vs Alpha-beta pruning #

Performance over 100 games:

Minimax: 27
Draw: 4
Alpha-beta: 69

Alpha-beta pruning vs Alpha-beta + presort #

Performance over 100 games:

Alpha-beta: 34
Draw: 3
Presort: 63

Minimax vs Alpha-beta + presort #

Performance over 100 games:

Minimax: 20
Draw: 4
Presort: 76

Clearly Alpha-beta pruning with move presort is the best performing AI (so far). The others are still able to win or draw games due to the significant stochastic component of the game (at the start of each round).

If you fancy your chances, you can play against it here